import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
from ipywidgets import *
%matplotlib inline
EDA
Let us make some elementary charts and plots to understand what the data is like.
df_PCOS_all = pd.read_excel('PCOS_data_without_infertility.xlsx', sheet_name = 'Full_new')
df_PCOS_all.head()
| Sl. No | Patient File No. | PCOS (Y/N) | Age (yrs) | Weight (Kg) | Height(Cm) | BMI | Blood Group | Pulse rate(bpm) | RR (breaths/min) | ... | Fast food (Y/N) | Reg.Exercise(Y/N) | BP _Systolic (mmHg) | BP _Diastolic (mmHg) | Follicle No. (L) | Follicle No. (R) | Avg. F size (L) (mm) | Avg. F size (R) (mm) | Endometrium (mm) | Unnamed: 44 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 0 | 28 | 44.6 | 152.0 | 19.300000 | 15 | 78 | 22 | ... | 1.0 | 0 | 110 | 80 | 3 | 3 | 18.0 | 18.0 | 8.5 | NaN |
| 1 | 2 | 2 | 0 | 36 | 65.0 | 161.5 | 24.921163 | 15 | 74 | 20 | ... | 0.0 | 0 | 120 | 70 | 3 | 5 | 15.0 | 14.0 | 3.7 | NaN |
| 2 | 3 | 3 | 1 | 33 | 68.8 | 165.0 | 25.270891 | 11 | 72 | 18 | ... | 1.0 | 0 | 120 | 80 | 13 | 15 | 18.0 | 20.0 | 10.0 | NaN |
| 3 | 4 | 4 | 0 | 37 | 65.0 | 148.0 | 29.674945 | 13 | 72 | 20 | ... | 0.0 | 0 | 120 | 70 | 2 | 2 | 15.0 | 14.0 | 7.5 | NaN |
| 4 | 5 | 5 | 0 | 25 | 52.0 | 161.0 | 20.060954 | 11 | 72 | 18 | ... | 0.0 | 0 | 120 | 80 | 3 | 4 | 16.0 | 14.0 | 7.0 | NaN |
5 rows × 45 columns
df_PCOS_all.describe()
| Sl. No | Patient File No. | PCOS (Y/N) | Age (yrs) | Weight (Kg) | Height(Cm) | BMI | Blood Group | Pulse rate(bpm) | RR (breaths/min) | ... | Pimples(Y/N) | Fast food (Y/N) | Reg.Exercise(Y/N) | BP _Systolic (mmHg) | BP _Diastolic (mmHg) | Follicle No. (L) | Follicle No. (R) | Avg. F size (L) (mm) | Avg. F size (R) (mm) | Endometrium (mm) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| count | 541.000000 | 541.000000 | 541.000000 | 541.000000 | 541.000000 | 541.000000 | 541.000000 | 541.000000 | 541.000000 | 541.000000 | ... | 541.000000 | 540.000000 | 541.000000 | 541.000000 | 541.000000 | 541.000000 | 541.000000 | 541.000000 | 541.000000 | 541.000000 |
| mean | 271.000000 | 271.000000 | 0.327172 | 31.430684 | 59.637153 | 156.484835 | 24.311285 | 13.802218 | 73.247689 | 19.243993 | ... | 0.489834 | 0.514815 | 0.247689 | 114.661738 | 76.927911 | 6.129390 | 6.641405 | 15.018115 | 15.451701 | 8.475915 |
| std | 156.317519 | 156.317519 | 0.469615 | 5.411006 | 11.028287 | 6.033545 | 4.056399 | 1.840812 | 4.430285 | 1.688629 | ... | 0.500359 | 0.500244 | 0.432070 | 7.384556 | 5.574112 | 4.229294 | 4.436889 | 3.566839 | 3.318848 | 2.165381 |
| min | 1.000000 | 1.000000 | 0.000000 | 20.000000 | 31.000000 | 137.000000 | 12.417882 | 11.000000 | 13.000000 | 16.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 12.000000 | 8.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 25% | 136.000000 | 136.000000 | 0.000000 | 28.000000 | 52.000000 | 152.000000 | 21.641274 | 13.000000 | 72.000000 | 18.000000 | ... | 0.000000 | 0.000000 | 0.000000 | 110.000000 | 70.000000 | 3.000000 | 3.000000 | 13.000000 | 13.000000 | 7.000000 |
| 50% | 271.000000 | 271.000000 | 0.000000 | 31.000000 | 59.000000 | 156.000000 | 24.238227 | 14.000000 | 72.000000 | 18.000000 | ... | 0.000000 | 1.000000 | 0.000000 | 110.000000 | 80.000000 | 5.000000 | 6.000000 | 15.000000 | 16.000000 | 8.500000 |
| 75% | 406.000000 | 406.000000 | 1.000000 | 35.000000 | 65.000000 | 160.000000 | 26.634958 | 15.000000 | 74.000000 | 20.000000 | ... | 1.000000 | 1.000000 | 0.000000 | 120.000000 | 80.000000 | 9.000000 | 10.000000 | 18.000000 | 18.000000 | 9.800000 |
| max | 541.000000 | 541.000000 | 1.000000 | 48.000000 | 108.000000 | 180.000000 | 38.900000 | 18.000000 | 82.000000 | 28.000000 | ... | 1.000000 | 1.000000 | 1.000000 | 140.000000 | 100.000000 | 22.000000 | 20.000000 | 24.000000 | 24.000000 | 18.000000 |
8 rows × 42 columns
df_PCOS_all.info()
<class 'pandas.core.frame.DataFrame'>
RangeIndex: 541 entries, 0 to 540
Data columns (total 45 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Sl. No 541 non-null int64
1 Patient File No. 541 non-null int64
2 PCOS (Y/N) 541 non-null int64
3 Age (yrs) 541 non-null int64
4 Weight (Kg) 541 non-null float64
5 Height(Cm) 541 non-null float64
6 BMI 541 non-null float64
7 Blood Group 541 non-null int64
8 Pulse rate(bpm) 541 non-null int64
9 RR (breaths/min) 541 non-null int64
10 Hb(g/dl) 541 non-null float64
11 Cycle(R/I) 541 non-null int64
12 Cycle length(days) 541 non-null int64
13 Marraige Status (Yrs) 540 non-null float64
14 Pregnant(Y/N) 541 non-null int64
15 No. of aborptions 541 non-null int64
16 I beta-HCG(mIU/mL) 541 non-null float64
17 II beta-HCG(mIU/mL) 541 non-null object
18 FSH(mIU/mL) 541 non-null float64
19 LH(mIU/mL) 541 non-null float64
20 FSH/LH 541 non-null float64
21 Hip(inch) 541 non-null int64
22 Waist(inch) 541 non-null int64
23 Waist:Hip Ratio 541 non-null float64
24 TSH (mIU/L) 541 non-null float64
25 AMH(ng/mL) 541 non-null object
26 PRL(ng/mL) 541 non-null float64
27 Vit D3 (ng/mL) 541 non-null float64
28 PRG(ng/mL) 541 non-null float64
29 RBS(mg/dl) 541 non-null float64
30 Weight gain(Y/N) 541 non-null int64
31 hair growth(Y/N) 541 non-null int64
32 Skin darkening (Y/N) 541 non-null int64
33 Hair loss(Y/N) 541 non-null int64
34 Pimples(Y/N) 541 non-null int64
35 Fast food (Y/N) 540 non-null float64
36 Reg.Exercise(Y/N) 541 non-null int64
37 BP _Systolic (mmHg) 541 non-null int64
38 BP _Diastolic (mmHg) 541 non-null int64
39 Follicle No. (L) 541 non-null int64
40 Follicle No. (R) 541 non-null int64
41 Avg. F size (L) (mm) 541 non-null float64
42 Avg. F size (R) (mm) 541 non-null float64
43 Endometrium (mm) 541 non-null float64
44 Unnamed: 44 2 non-null object
dtypes: float64(19), int64(23), object(3)
memory usage: 190.3+ KB
print(df_PCOS_all["Marraige Status (Yrs)"].isnull().sum())
index = df_PCOS_all.index[df_PCOS_all['AMH(ng/mL)'] == "a"]
df_PCOS_all = df_PCOS_all.drop(index)
Let’s find all the missing values
Let us convert the Y/N columns to boolean type.
df_PCOS_all["Cycle(R/I)"] = np.where(df_PCOS_all["Cycle(R/I)"] > 2, True, False)
columns_to_convert = df_PCOS_all.filter(like = 'Y/N').columns
df_PCOS_all[columns_to_convert] = df_PCOS_all[columns_to_convert].astype('bool')
Let us check if it has worked.
df_PCOS_all.info()
<class 'pandas.core.frame.DataFrame'>
Index: 540 entries, 0 to 540
Data columns (total 45 columns):
# Column Non-Null Count Dtype
--- ------ -------------- -----
0 Sl. No 540 non-null int64
1 Patient File No. 540 non-null int64
2 PCOS (Y/N) 540 non-null bool
3 Age (yrs) 540 non-null int64
4 Weight (Kg) 540 non-null float64
5 Height(Cm) 540 non-null float64
6 BMI 540 non-null float64
7 Blood Group 540 non-null int64
8 Pulse rate(bpm) 540 non-null int64
9 RR (breaths/min) 540 non-null int64
10 Hb(g/dl) 540 non-null float64
11 Cycle(R/I) 540 non-null bool
12 Cycle length(days) 540 non-null int64
13 Marraige Status (Yrs) 539 non-null float64
14 Pregnant(Y/N) 540 non-null bool
15 No. of aborptions 540 non-null int64
16 I beta-HCG(mIU/mL) 540 non-null float64
17 II beta-HCG(mIU/mL) 540 non-null object
18 FSH(mIU/mL) 540 non-null float64
19 LH(mIU/mL) 540 non-null float64
20 FSH/LH 540 non-null float64
21 Hip(inch) 540 non-null int64
22 Waist(inch) 540 non-null int64
23 Waist:Hip Ratio 540 non-null float64
24 TSH (mIU/L) 540 non-null float64
25 AMH(ng/mL) 540 non-null object
26 PRL(ng/mL) 540 non-null float64
27 Vit D3 (ng/mL) 540 non-null float64
28 PRG(ng/mL) 540 non-null float64
29 RBS(mg/dl) 540 non-null float64
30 Weight gain(Y/N) 540 non-null bool
31 hair growth(Y/N) 540 non-null bool
32 Skin darkening (Y/N) 540 non-null bool
33 Hair loss(Y/N) 540 non-null bool
34 Pimples(Y/N) 540 non-null bool
35 Fast food (Y/N) 540 non-null bool
36 Reg.Exercise(Y/N) 540 non-null bool
37 BP _Systolic (mmHg) 540 non-null int64
38 BP _Diastolic (mmHg) 540 non-null int64
39 Follicle No. (L) 540 non-null int64
40 Follicle No. (R) 540 non-null int64
41 Avg. F size (L) (mm) 540 non-null float64
42 Avg. F size (R) (mm) 540 non-null float64
43 Endometrium (mm) 540 non-null float64
44 Unnamed: 44 2 non-null object
dtypes: bool(10), float64(18), int64(14), object(3)
memory usage: 173.3+ KB
Data Cleaning
Apparently there is one numeric value mis-typed as 1.99. rather than 1.99 which makes it difficult for the column to be converted to float, let’s correct that.
print(df_PCOS_all['II beta-HCG(mIU/mL)'] == "1.99.")
print(df_PCOS_all.loc[123, 'II beta-HCG(mIU/mL)'])
df_PCOS_all.loc[123, 'II beta-HCG(mIU/mL)'] = '1.99'
#df_PCOS_all = df_PCOS_all.drop(302)
print(df_PCOS_all.loc[123, 'II beta-HCG(mIU/mL)'])
0 False
1 False
2 False
3 False
4 False
...
536 False
537 False
538 False
539 False
540 False
Name: II beta-HCG(mIU/mL), Length: 540, dtype: bool
1.99.
1.99
First visualisations
Make some plots to understand how the data looks like
columns_to_drop = ['Unnamed: 44', 'Sl. No', 'Patient File No.', 'Blood Group']
#columns_to_drop = ['Sl. No', 'Patient File No.', 'Blood Group']
df_temp = df_PCOS_all.select_dtypes(exclude = 'bool')
df_temp = df_temp.drop(columns_to_drop, axis = 1)
#df_temp = df_temp.drop[df_temp.index[df_temp['AMH(ng/mL)'] == "a"]]
df_temp[df_temp.columns] = df_temp[df_temp.columns].astype('float64')
variables = Dropdown(options = list(df_temp.columns), description = 'Variables')
output = Output()
def make_plot(*args):
output.clear_output(wait=True)
with output:
sns.histplot(x = variables.value, data= df_temp, kde = True)
plt.show()
variables.observe(make_plot, names = 'value')
display(variables, output)
Dropdown(description='Variables', options=(' Age (yrs)', 'Weight (Kg)', 'Height(Cm) ', 'BMI', 'Pulse rate(bpm)…
Output()
Finding correlations
Let’s understand the correlations
sns.clustermap(df_temp.corr(), cmap="rocket_r")
<seaborn.matrix.ClusterGrid at 0x13bf76a50>
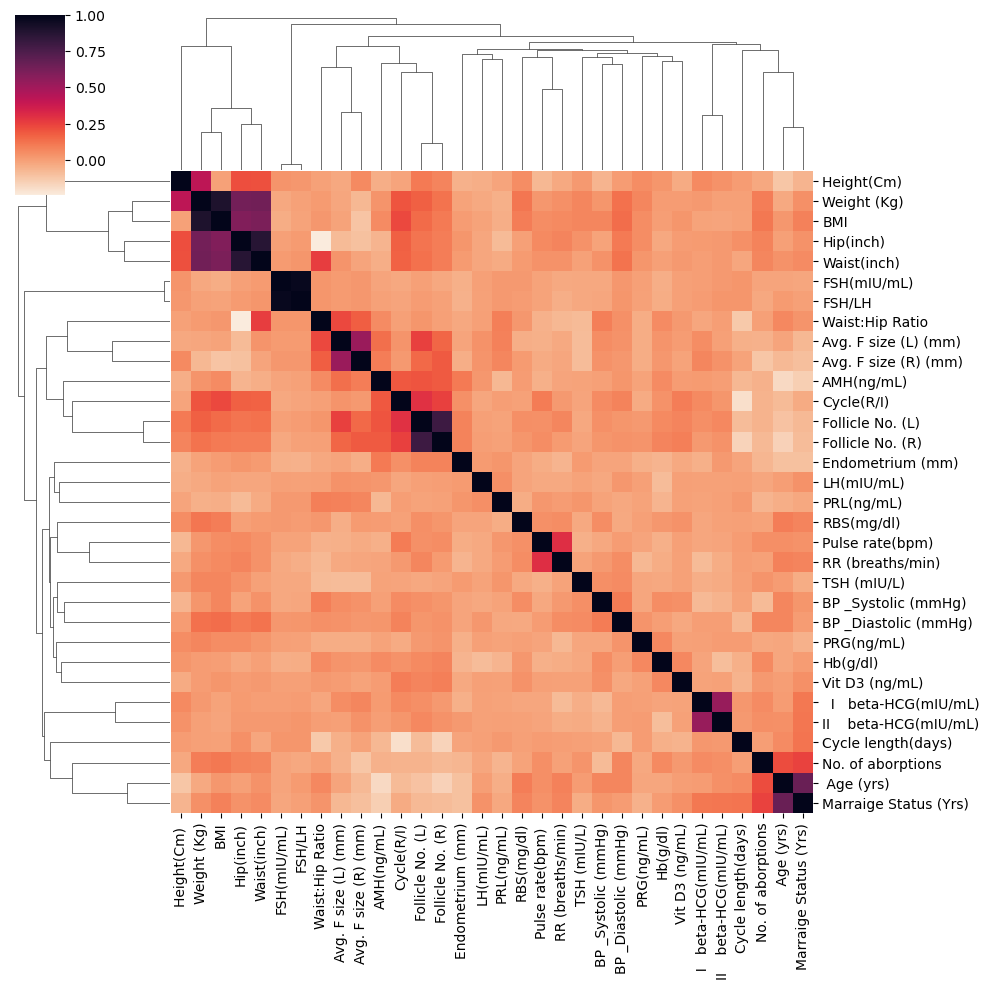
df_temp.corr().style.background_gradient(cmap='coolwarm')
| Age (yrs) | Weight (Kg) | Height(Cm) | BMI | Pulse rate(bpm) | RR (breaths/min) | Hb(g/dl) | Cycle(R/I) | Cycle length(days) | Marraige Status (Yrs) | No. of aborptions | I beta-HCG(mIU/mL) | II beta-HCG(mIU/mL) | FSH(mIU/mL) | LH(mIU/mL) | FSH/LH | Hip(inch) | Waist(inch) | Waist:Hip Ratio | TSH (mIU/L) | AMH(ng/mL) | PRL(ng/mL) | Vit D3 (ng/mL) | PRG(ng/mL) | RBS(mg/dl) | BP _Systolic (mmHg) | BP _Diastolic (mmHg) | Follicle No. (L) | Follicle No. (R) | Avg. F size (L) (mm) | Avg. F size (R) (mm) | Endometrium (mm) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Age (yrs) | 1.000000 | -0.029136 | -0.118577 | 0.021316 | 0.045553 | 0.086628 | -0.022778 | -0.084871 | 0.055898 | 0.662254 | 0.221843 | 0.008511 | 0.043378 | -0.017708 | 0.000603 | 0.012432 | -0.001346 | 0.036263 | 0.066452 | 0.010245 | -0.179648 | -0.046077 | 0.004454 | -0.021775 | 0.097086 | 0.072313 | 0.069329 | -0.109965 | -0.158865 | -0.017435 | -0.079646 | -0.101969 |
| Weight (Kg) | -0.029136 | 1.000000 | 0.419901 | 0.901755 | 0.020089 | 0.043901 | 0.009979 | 0.200470 | -0.002284 | 0.043991 | 0.093310 | 0.015882 | -0.000521 | -0.025785 | -0.029910 | -0.004831 | 0.633920 | 0.639589 | 0.014976 | 0.071410 | 0.031050 | -0.050016 | 0.008145 | 0.069688 | 0.114294 | 0.028066 | 0.130843 | 0.173501 | 0.124092 | -0.021036 | -0.073115 | -0.010932 |
| Height(Cm) | -0.118577 | 0.419901 | 1.000000 | -0.006906 | -0.074144 | -0.028862 | 0.025259 | -0.018208 | 0.009595 | -0.066407 | -0.026240 | 0.062079 | 0.036474 | 0.030883 | -0.045619 | 0.022065 | 0.215357 | 0.209348 | -0.008982 | 0.018501 | -0.045208 | -0.018178 | -0.034997 | 0.049654 | 0.050437 | -0.067029 | 0.009420 | 0.105574 | 0.074896 | -0.025959 | 0.059686 | -0.055987 |
| BMI | 0.021316 | 0.901755 | -0.006906 | 1.000000 | 0.050536 | 0.061932 | 0.003534 | 0.232891 | -0.006231 | 0.084015 | 0.109865 | -0.009967 | -0.015270 | -0.040717 | -0.013312 | -0.012076 | 0.597058 | 0.607524 | 0.023602 | 0.072305 | 0.054023 | -0.047721 | 0.027035 | 0.049460 | 0.093543 | 0.069549 | 0.140134 | 0.142903 | 0.104205 | -0.011594 | -0.111519 | 0.009320 |
| Pulse rate(bpm) | 0.045553 | 0.020089 | -0.074144 | 0.050536 | 1.000000 | 0.303727 | -0.052265 | 0.101241 | 0.006411 | 0.038701 | 0.046227 | -0.020437 | -0.016226 | -0.013071 | -0.032315 | -0.013104 | 0.062951 | 0.037880 | -0.052890 | -0.051482 | -0.049843 | 0.020750 | -0.001486 | -0.017678 | 0.042002 | -0.025751 | 0.008027 | 0.040559 | 0.049307 | -0.048546 | -0.034256 | -0.040891 |
| RR (breaths/min) | 0.086628 | 0.043901 | -0.028862 | 0.061932 | 0.303727 | 1.000000 | -0.041027 | 0.018850 | 0.004972 | 0.077701 | -0.006090 | -0.085028 | -0.039017 | -0.032388 | -0.031211 | -0.043339 | 0.075020 | 0.038310 | -0.075567 | -0.011968 | -0.017480 | 0.007284 | -0.009016 | -0.076895 | 0.050811 | 0.016734 | 0.053751 | 0.070179 | 0.012752 | -0.031527 | -0.022035 | -0.062941 |
| Hb(g/dl) | -0.022778 | 0.009979 | 0.025259 | 0.003534 | -0.052265 | -0.041027 | 1.000000 | 0.037428 | -0.051992 | 0.006743 | 0.060702 | -0.016649 | -0.094425 | -0.047398 | -0.089107 | -0.039827 | -0.024712 | -0.000779 | 0.057161 | -0.026156 | 0.056172 | -0.063091 | 0.063916 | 0.065769 | 0.024067 | 0.052229 | 0.002046 | 0.061814 | 0.073422 | 0.031995 | 0.024153 | -0.065041 |
| Cycle(R/I) | -0.084871 | 0.200470 | -0.018208 | 0.232891 | 0.101241 | 0.018850 | 0.037428 | 1.000000 | -0.201044 | -0.033557 | -0.057937 | 0.063098 | 0.027930 | -0.026083 | -0.021393 | -0.016167 | 0.174305 | 0.168856 | -0.004003 | -0.017435 | 0.194063 | 0.005251 | 0.096717 | -0.033781 | -0.006394 | 0.055790 | 0.080057 | 0.296114 | 0.251271 | 0.034112 | 0.016204 | 0.042168 |
| Cycle length(days) | 0.055898 | -0.002284 | 0.009595 | -0.006231 | 0.006411 | 0.004972 | -0.051992 | -0.201044 | 1.000000 | 0.117850 | 0.004023 | 0.020187 | 0.018577 | 0.029645 | -0.001686 | 0.025937 | 0.040354 | -0.023479 | -0.130093 | -0.003191 | -0.072822 | 0.016415 | -0.058345 | 0.007190 | 0.000210 | -0.011963 | -0.075792 | -0.086809 | -0.161256 | -0.052364 | -0.013956 | -0.016506 |
| Marraige Status (Yrs) | 0.662254 | 0.043991 | -0.066407 | 0.084015 | 0.038701 | 0.077701 | 0.006743 | -0.033557 | 0.117850 | 1.000000 | 0.246713 | 0.111666 | 0.112905 | -0.023461 | 0.035509 | -0.002983 | 0.038325 | 0.057376 | 0.033334 | -0.040241 | -0.146482 | -0.025819 | 0.041541 | -0.052840 | 0.075519 | 0.028478 | 0.005745 | -0.079079 | -0.087227 | -0.072229 | -0.097536 | -0.105882 |
| No. of aborptions | 0.221843 | 0.093310 | -0.026240 | 0.109865 | 0.046227 | -0.006090 | 0.060702 | -0.057937 | 0.004023 | 0.246713 | 1.000000 | 0.057762 | 0.046977 | -0.018187 | -0.018876 | -0.026472 | 0.078418 | 0.073280 | -0.004031 | 0.032359 | -0.052920 | -0.064655 | 0.015516 | -0.023962 | -0.013134 | -0.083221 | 0.070745 | -0.058061 | -0.078688 | -0.056589 | -0.117573 | -0.067758 |
| I beta-HCG(mIU/mL) | 0.008511 | 0.015882 | 0.062079 | -0.009967 | -0.020437 | -0.085028 | -0.016649 | 0.063098 | 0.020187 | 0.111666 | 0.057762 | 1.000000 | 0.533687 | 0.001641 | -0.006914 | 0.007892 | 0.014833 | 0.005173 | -0.021490 | -0.044710 | 0.014428 | -0.013383 | -0.012659 | -0.002984 | -0.023509 | -0.081720 | 0.003923 | 0.048325 | 0.018266 | 0.050100 | 0.071863 | -0.051920 |
| II beta-HCG(mIU/mL) | 0.043378 | -0.000521 | 0.036474 | -0.015270 | -0.016226 | -0.039017 | -0.094425 | 0.027930 | 0.018577 | 0.112905 | 0.046977 | 0.533687 | 1.000000 | 0.016752 | -0.008092 | 0.027150 | 0.015716 | 0.016541 | 0.001982 | -0.036839 | 0.003668 | -0.001337 | -0.007552 | 0.005649 | -0.004830 | -0.059202 | 0.004021 | 0.064106 | 0.037524 | 0.000003 | 0.037088 | 0.017013 |
| FSH(mIU/mL) | -0.017708 | -0.025785 | 0.030883 | -0.040717 | -0.013071 | -0.032388 | -0.047398 | -0.026083 | 0.029645 | -0.023461 | -0.018187 | 0.001641 | 0.016752 | 1.000000 | -0.001450 | 0.971951 | -0.000158 | 0.013754 | 0.027308 | -0.024805 | -0.014568 | 0.017848 | -0.000683 | -0.003426 | 0.018798 | -0.026830 | 0.023285 | -0.002342 | -0.025358 | 0.011547 | 0.020184 | -0.049158 |
| LH(mIU/mL) | 0.000603 | -0.029910 | -0.045619 | -0.013312 | -0.032315 | -0.031211 | -0.089107 | -0.021393 | -0.001686 | 0.035509 | -0.018876 | -0.006914 | -0.008092 | -0.001450 | 1.000000 | -0.005724 | -0.021727 | -0.022304 | -0.002980 | -0.009398 | 0.021055 | 0.046904 | -0.001543 | -0.004080 | -0.015216 | -0.027699 | 0.023964 | -0.001280 | 0.003430 | 0.035632 | 0.032495 | 0.010786 |
| FSH/LH | 0.012432 | -0.004831 | 0.022065 | -0.012076 | -0.013104 | -0.043339 | -0.039827 | -0.016167 | 0.025937 | -0.002983 | -0.026472 | 0.007892 | 0.027150 | 0.971951 | -0.005724 | 1.000000 | 0.012370 | 0.027588 | 0.029240 | -0.028331 | -0.007438 | 0.015264 | -0.001750 | -0.005109 | 0.006231 | -0.019302 | 0.026920 | 0.005872 | -0.007506 | 0.014923 | 0.024070 | -0.053768 |
| Hip(inch) | -0.001346 | 0.633920 | 0.215357 | 0.597058 | 0.062951 | 0.075020 | -0.024712 | 0.174305 | 0.040354 | 0.038325 | 0.078418 | 0.014833 | 0.015716 | -0.000158 | -0.021727 | 0.012370 | 1.000000 | 0.873589 | -0.241990 | 0.035835 | -0.066106 | -0.082153 | 0.009742 | 0.050008 | -0.001393 | -0.012106 | 0.104944 | 0.119505 | 0.094799 | -0.082276 | -0.104384 | 0.027778 |
| Waist(inch) | 0.036263 | 0.639589 | 0.209348 | 0.607524 | 0.037880 | 0.038310 | -0.000779 | 0.168856 | -0.023479 | 0.057376 | 0.073280 | 0.005173 | 0.016541 | 0.013754 | -0.022304 | 0.027588 | 0.873589 | 1.000000 | 0.258365 | -0.008295 | -0.043132 | -0.036364 | 0.018989 | 0.029175 | 0.012995 | 0.034558 | 0.125243 | 0.129846 | 0.093401 | 0.031048 | -0.015271 | 0.012810 |
| Waist:Hip Ratio | 0.066452 | 0.014976 | -0.008982 | 0.023602 | -0.052890 | -0.075567 | 0.057161 | -0.004003 | -0.130093 | 0.033334 | -0.004031 | -0.021490 | 0.001982 | 0.027308 | -0.002980 | 0.029240 | -0.241990 | 0.258365 | 1.000000 | -0.085023 | 0.057354 | 0.092356 | 0.017701 | -0.039042 | 0.023170 | 0.088978 | 0.042507 | 0.026456 | -0.002207 | 0.229355 | 0.176453 | -0.026793 |
| TSH (mIU/L) | 0.010245 | 0.071410 | 0.018501 | 0.072305 | -0.051482 | -0.011968 | -0.026156 | -0.017435 | -0.003191 | -0.040241 | 0.032359 | -0.044710 | -0.036839 | -0.024805 | -0.009398 | -0.028331 | 0.035835 | -0.008295 | -0.085023 | 1.000000 | -0.010854 | 0.025606 | -0.009114 | -0.020504 | -0.030056 | 0.048215 | 0.055034 | -0.028164 | -0.016807 | -0.091201 | -0.088850 | 0.013863 |
| AMH(ng/mL) | -0.179648 | 0.031050 | -0.045208 | 0.054023 | -0.049843 | -0.017480 | 0.056172 | 0.194063 | -0.072822 | -0.146482 | -0.052920 | 0.014428 | 0.003668 | -0.014568 | 0.021055 | -0.007438 | -0.066106 | -0.043132 | 0.057354 | -0.010854 | 1.000000 | -0.072214 | 0.007660 | -0.011195 | 0.008454 | -0.003192 | 0.026038 | 0.203407 | 0.188537 | 0.134628 | 0.096079 | 0.104159 |
| PRL(ng/mL) | -0.046077 | -0.050016 | -0.018178 | -0.047721 | 0.020750 | 0.007284 | -0.063091 | 0.005251 | 0.016415 | -0.025819 | -0.064655 | -0.013383 | -0.001337 | 0.017848 | 0.046904 | 0.015264 | -0.082153 | -0.036364 | 0.092356 | 0.025606 | -0.072214 | 1.000000 | -0.006827 | -0.009700 | -0.041676 | -0.009963 | -0.026821 | -0.010803 | -0.008607 | 0.086311 | 0.071688 | 0.027439 |
| Vit D3 (ng/mL) | 0.004454 | 0.008145 | -0.034997 | 0.027035 | -0.001486 | -0.009016 | 0.063916 | 0.096717 | -0.058345 | 0.041541 | 0.015516 | -0.012659 | -0.007552 | -0.000683 | -0.001543 | -0.001750 | 0.009742 | 0.018989 | 0.017701 | -0.009114 | 0.007660 | -0.006827 | 1.000000 | -0.007240 | 0.038980 | 0.042855 | -0.024962 | 0.074172 | 0.091775 | 0.005441 | -0.011812 | -0.031385 |
| PRG(ng/mL) | -0.021775 | 0.069688 | 0.049654 | 0.049460 | -0.017678 | -0.076895 | 0.065769 | -0.033781 | 0.007190 | -0.052840 | -0.023962 | -0.002984 | 0.005649 | -0.003426 | -0.004080 | -0.005109 | 0.050008 | 0.029175 | -0.039042 | -0.020504 | -0.011195 | -0.009700 | -0.007240 | 1.000000 | -0.003545 | -0.020638 | 0.032131 | 0.018489 | 0.031483 | -0.040698 | -0.040910 | -0.047987 |
| RBS(mg/dl) | 0.097086 | 0.114294 | 0.050437 | 0.093543 | 0.042002 | 0.050811 | 0.024067 | -0.006394 | 0.000210 | 0.075519 | -0.013134 | -0.023509 | -0.004830 | 0.018798 | -0.015216 | 0.006231 | -0.001393 | 0.012995 | 0.023170 | -0.030056 | 0.008454 | -0.041676 | 0.038980 | -0.003545 | 1.000000 | 0.052683 | -0.032907 | 0.044342 | 0.027562 | -0.046821 | 0.013137 | -0.018700 |
| BP _Systolic (mmHg) | 0.072313 | 0.028066 | -0.067029 | 0.069549 | -0.025751 | 0.016734 | 0.052229 | 0.055790 | -0.011963 | 0.028478 | -0.083221 | -0.081720 | -0.059202 | -0.026830 | -0.027699 | -0.019302 | -0.012106 | 0.034558 | 0.088978 | 0.048215 | -0.003192 | -0.009963 | 0.042855 | -0.020638 | 0.052683 | 1.000000 | 0.102090 | 0.039463 | 0.025515 | 0.051273 | 0.038448 | -0.018613 |
| BP _Diastolic (mmHg) | 0.069329 | 0.130843 | 0.009420 | 0.140134 | 0.008027 | 0.053751 | 0.002046 | 0.080057 | -0.075792 | 0.005745 | 0.070745 | 0.003923 | 0.004021 | 0.023285 | 0.023964 | 0.026920 | 0.104944 | 0.125243 | 0.042507 | 0.055034 | 0.026038 | -0.026821 | -0.024962 | 0.032131 | -0.032907 | 0.102090 | 1.000000 | 0.025043 | 0.037844 | 0.037028 | 0.024013 | -0.015342 |
| Follicle No. (L) | -0.109965 | 0.173501 | 0.105574 | 0.142903 | 0.040559 | 0.070179 | 0.061814 | 0.296114 | -0.086809 | -0.079079 | -0.058061 | 0.048325 | 0.064106 | -0.002342 | -0.001280 | 0.005872 | 0.119505 | 0.129846 | 0.026456 | -0.028164 | 0.203407 | -0.010803 | 0.074172 | 0.018489 | 0.044342 | 0.039463 | 0.025043 | 1.000000 | 0.799516 | 0.249781 | 0.149002 | 0.078605 |
| Follicle No. (R) | -0.158865 | 0.124092 | 0.074896 | 0.104205 | 0.049307 | 0.012752 | 0.073422 | 0.251271 | -0.161256 | -0.087227 | -0.078688 | 0.018266 | 0.037524 | -0.025358 | 0.003430 | -0.007506 | 0.094799 | 0.093401 | -0.002207 | -0.016807 | 0.188537 | -0.008607 | 0.091775 | 0.031483 | 0.027562 | 0.025515 | 0.037844 | 0.799516 | 1.000000 | 0.156640 | 0.188049 | 0.079817 |
| Avg. F size (L) (mm) | -0.017435 | -0.021036 | -0.025959 | -0.011594 | -0.048546 | -0.031527 | 0.031995 | 0.034112 | -0.052364 | -0.072229 | -0.056589 | 0.050100 | 0.000003 | 0.011547 | 0.035632 | 0.014923 | -0.082276 | 0.031048 | 0.229355 | -0.091201 | 0.134628 | 0.086311 | 0.005441 | -0.040698 | -0.046821 | 0.051273 | 0.037028 | 0.249781 | 0.156640 | 1.000000 | 0.522794 | -0.014174 |
| Avg. F size (R) (mm) | -0.079646 | -0.073115 | 0.059686 | -0.111519 | -0.034256 | -0.022035 | 0.024153 | 0.016204 | -0.013956 | -0.097536 | -0.117573 | 0.071863 | 0.037088 | 0.020184 | 0.032495 | 0.024070 | -0.104384 | -0.015271 | 0.176453 | -0.088850 | 0.096079 | 0.071688 | -0.011812 | -0.040910 | 0.013137 | 0.038448 | 0.024013 | 0.149002 | 0.188049 | 0.522794 | 1.000000 | -0.045628 |
| Endometrium (mm) | -0.101969 | -0.010932 | -0.055987 | 0.009320 | -0.040891 | -0.062941 | -0.065041 | 0.042168 | -0.016506 | -0.105882 | -0.067758 | -0.051920 | 0.017013 | -0.049158 | 0.010786 | -0.053768 | 0.027778 | 0.012810 | -0.026793 | 0.013863 | 0.104159 | 0.027439 | -0.031385 | -0.047987 | -0.018700 | -0.018613 | -0.015342 | 0.078605 | 0.079817 | -0.014174 | -0.045628 | 1.000000 |
Correlation analysis
So far we did nott split the data on PCOS diagnosis. Our next task is to do that. Let’s make to different dataframes:
- contains PCOS diagnosis
- does not contain PCOS diagnosis
This should not be strictly necessary, but I am just playing around pandas here.
df_PCOS = df_PCOS_all[df_PCOS_all['PCOS (Y/N)']]
df_no_PCOS = df_PCOS_all[~df_PCOS_all['PCOS (Y/N)']]
df_no_PCOS
| Sl. No | Patient File No. | PCOS (Y/N) | Age (yrs) | Weight (Kg) | Height(Cm) | BMI | Blood Group | Pulse rate(bpm) | RR (breaths/min) | ... | Fast food (Y/N) | Reg.Exercise(Y/N) | BP _Systolic (mmHg) | BP _Diastolic (mmHg) | Follicle No. (L) | Follicle No. (R) | Avg. F size (L) (mm) | Avg. F size (R) (mm) | Endometrium (mm) | Unnamed: 44 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | False | 28 | 44.6 | 152.000 | 19.300000 | 15 | 78 | 22 | ... | True | False | 110 | 80 | 3 | 3 | 18.0 | 18.0 | 8.5 | NaN |
| 1 | 2 | 2 | False | 36 | 65.0 | 161.500 | 24.921163 | 15 | 74 | 20 | ... | False | False | 120 | 70 | 3 | 5 | 15.0 | 14.0 | 3.7 | NaN |
| 3 | 4 | 4 | False | 37 | 65.0 | 148.000 | 29.674945 | 13 | 72 | 20 | ... | False | False | 120 | 70 | 2 | 2 | 15.0 | 14.0 | 7.5 | NaN |
| 4 | 5 | 5 | False | 25 | 52.0 | 161.000 | 20.060954 | 11 | 72 | 18 | ... | False | False | 120 | 80 | 3 | 4 | 16.0 | 14.0 | 7.0 | NaN |
| 5 | 6 | 6 | False | 36 | 74.1 | 165.000 | 27.217631 | 15 | 78 | 28 | ... | False | False | 110 | 70 | 9 | 6 | 16.0 | 20.0 | 8.0 | NaN |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 535 | 536 | 536 | False | 26 | 80.0 | 161.544 | 30.700000 | 18 | 70 | 18 | ... | False | False | 110 | 80 | 7 | 9 | 13.0 | 17.5 | 9.6 | NaN |
| 536 | 537 | 537 | False | 35 | 50.0 | 164.592 | 18.500000 | 17 | 72 | 16 | ... | False | False | 110 | 70 | 1 | 0 | 17.5 | 10.0 | 6.7 | NaN |
| 537 | 538 | 538 | False | 30 | 63.2 | 158.000 | 25.300000 | 15 | 72 | 18 | ... | False | False | 110 | 70 | 9 | 7 | 19.0 | 18.0 | 8.2 | NaN |
| 538 | 539 | 539 | False | 36 | 54.0 | 152.000 | 23.400000 | 13 | 74 | 20 | ... | False | False | 110 | 80 | 1 | 0 | 18.0 | 9.0 | 7.3 | NaN |
| 539 | 540 | 540 | False | 27 | 50.0 | 150.000 | 22.200000 | 15 | 74 | 20 | ... | False | False | 110 | 70 | 7 | 6 | 18.0 | 16.0 | 11.5 | NaN |
363 rows × 45 columns
# We have to use Perason's correlation coefficient because the dataframe contains both boolean and integer values.
corr = df_PCOS_all.drop(columns_to_drop, axis = 1).corr(method ='pearson')
# Let's try to extract the variables which have the highest and lowest correlation with PCOS status.
print(f' The three highest {list(corr.nlargest(3, "PCOS (Y/N)")["PCOS (Y/N)"].index)}')
print(f' The three smallest PCOS correlated variables are {list(corr.nsmallest(3, "PCOS (Y/N)")["PCOS (Y/N)"].index)}')
The three highest ['PCOS (Y/N)', 'Follicle No. (R)', 'Follicle No. (L)']
The three smallest PCOS correlated variables are ['Cycle length(days)', ' Age (yrs)', 'Marraige Status (Yrs)']
Checking the positive and negative correlations seperately
Do the correlation matrices of PCOS diagnosis vs no PCOS diagnosis look very different?
corrpos = df_PCOS.drop(columns_to_drop, axis = 1).corr()
corrneg = df_no_PCOS.drop(columns_to_drop, axis = 1).corr()
sns.heatmap(corrpos, cmap="Pastel1")
plt.title('Correlations in PCOS diagosed data');
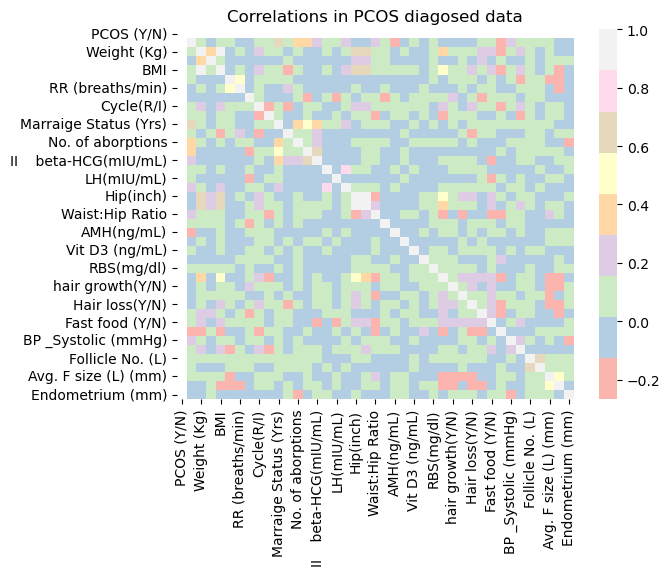
sns.heatmap(corrneg, cmap="Pastel1")
plt.title('Correlations in no PCOS diagosed data');
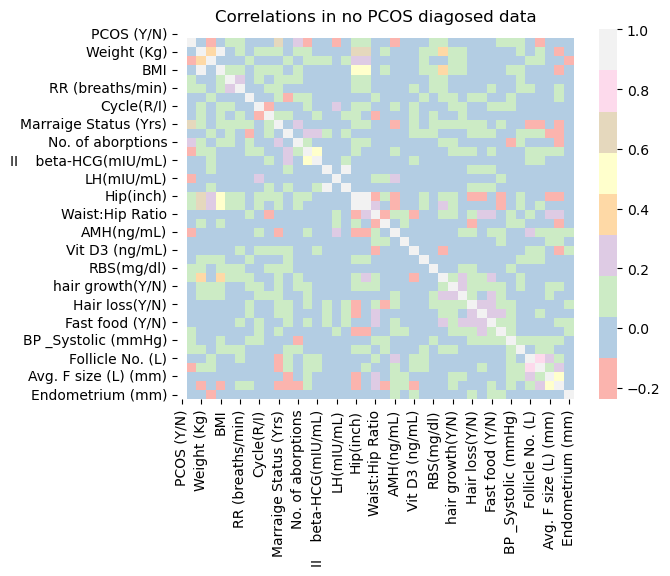
sns.heatmap(corrpos-corrneg, cmap="Pastel1")
plt.title('Difference between PCOS diagnosed and no PCOS diagnose data');
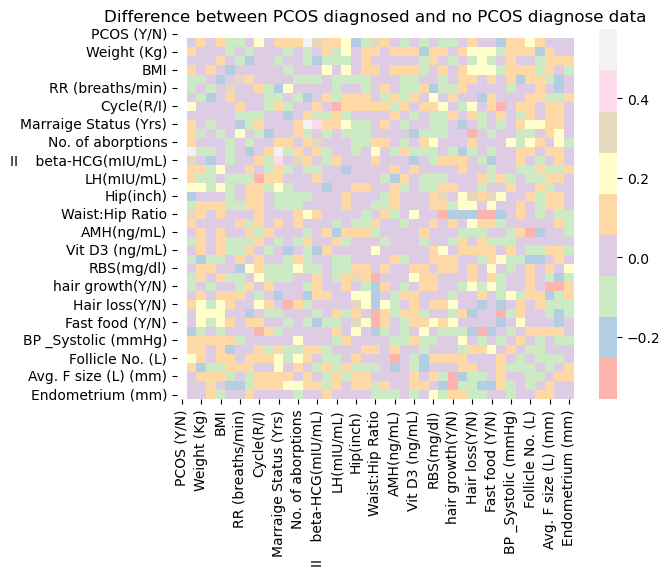
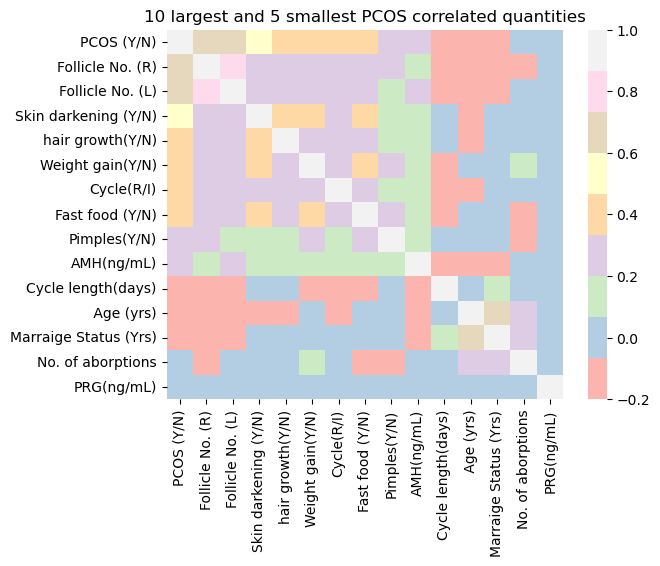
For simplicity I would want to plot the 10 highest PCOS correlated and 5 lowest correlated variables as a heatmap.
#print(df_PCOS_all.describe())
#columns_to_drop = ['Sl. No', 'Patient File No.', 'Blood Group']
largest_vars = corr.nlargest(10, "PCOS (Y/N)")["PCOS (Y/N)"].index
smallest_vars = corr.nsmallest(5, "PCOS (Y/N)")["PCOS (Y/N)"].index
total_vars = largest_vars.append(smallest_vars)
sns.heatmap(df_PCOS_all.drop(columns_to_drop, axis=1)[total_vars].corr(), \
cmap = "Pastel1")
plt.title('10 largest and 5 smallest PCOS correlated quantities');
Visualise PCOS true and PCOS false data distributions
df_PCOS_numeric = df_PCOS.select_dtypes(exclude = 'bool')
df_PCOS_numeric = df_PCOS_numeric.drop(columns_to_drop, axis = 1)
df_no_PCOS_numeric = df_no_PCOS.select_dtypes(exclude = 'bool')
df_no_PCOS_numeric = df_no_PCOS_numeric.drop(columns_to_drop, axis = 1)
variable_dropdown = Dropdown(options = df_PCOS_numeric.columns)
output_plot = Output()
def make_histograms(*args):
output_plot.clear_output(wait = True)
with output_plot:
fig, ax1 = plt.subplots()
sns.histplot(x = variable_dropdown.value, data = df_PCOS, kde = True, ax = ax1 )
sns.histplot(x = variable_dropdown.value, data = df_no_PCOS, kde = True, ax = ax1)
#ax1.get_legend()
#legend = ax1.get_legend()
#handles = legend.legend_handles
#ax1.legend(handles, ['PCOS True', 'PCOS False'], title='Stat.ind.')
plt.show()
variable_dropdown.observe(make_histograms, names = 'value')
display(variable_dropdown, output_plot)
Dropdown(options=(' Age (yrs)', 'Weight (Kg)', 'Height(Cm) ', 'BMI', 'Pulse rate(bpm) ', 'RR (breaths/min)', '…
Output()
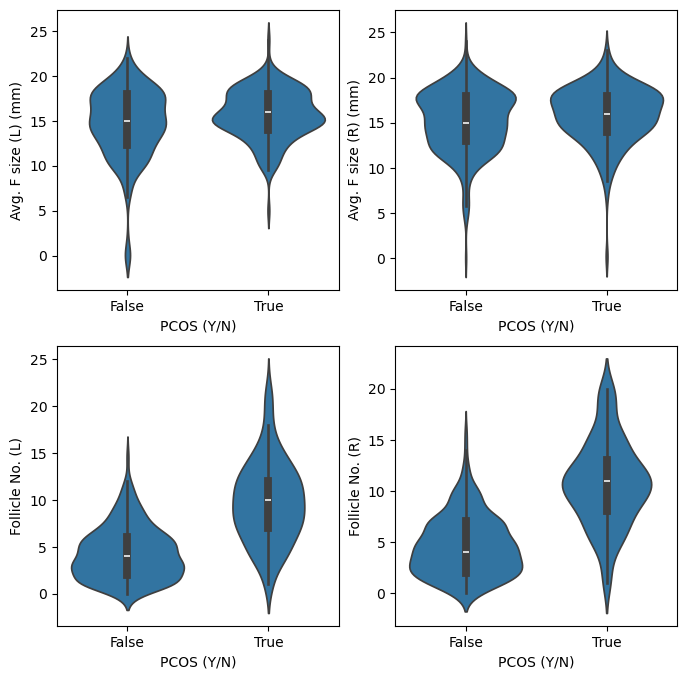
Among all the plots we can look at above the plots related to left and right follicle measurements are distinctly different. Let’s look at them in a bit more detail.
fig, ax = plt.subplots(2,2, figsize = (8,8))
sns.violinplot(df_PCOS_all, x = 'PCOS (Y/N)', y = 'Avg. F size (L) (mm)', ax = ax[0][0])
sns.violinplot(df_PCOS_all, x = 'PCOS (Y/N)', y = 'Avg. F size (R) (mm)', ax = ax[0][1])
sns.violinplot(df_PCOS_all, x = 'PCOS (Y/N)', y = 'Follicle No. (L)', ax = ax[1][0])
sns.violinplot(df_PCOS_all, x = 'PCOS (Y/N)', y = 'Follicle No. (R)', ax = ax[1][1])
<Axes: xlabel='PCOS (Y/N)', ylabel='Follicle No. (R)'>
Statistical analysis
My main goal is to be able to understand which factors are correlated with PCOS. These are not ‘causes’ of PCOS but rather symtoms which can help diagnose the condition. Note that correlations within binary data are also computed in .corr() method of pandas. Here I evaluate them explicitly.
Evaluating Cramér’s V coefficient
Cramér’s V coefficient is used for evaluating correlation between two variables. The variables may have more than binary categories. For variables A, B if
$n_{i,j}$ = number of times $A_i, B_j$ were observed,
$\chi^2 = \sum_{i,j}\frac{(n_{i,j} - {\frac{n_i, n_j}{n}})}{\frac{n_i, n_j}{n}}$
where $n_i = \sum_j n_{i,j}$ is the number of times the value $A_i$ is observed and $n_i = \sum_j n_{i,j}$ is the number of times the value $B_j$ is observed.
The coefficient is the computed as
$V = \sqrt\frac{\chi^2/n}{min(k-1)(r-1)}$
where $k$ = number of columns, $r$ = number of rows, $n$ = total number of observations
from scipy.stats import chi2_contingency
from tabulate import tabulate
import numpy as np
df_PCOS_bool = df_PCOS_all.select_dtypes(include = 'bool')
results = []
for col in df_PCOS_bool.columns:
if col == 'PCOS (Y/N)': continue
pearson_corr = df_PCOS_bool['PCOS (Y/N)'].astype(int).corr(df_PCOS_bool[col].astype(int))
# Now let's compute the Cramér's V coefficient
contigency_table = pd.crosstab(df_PCOS_bool['PCOS (Y/N)'].astype(int), df_PCOS_bool[col].astype(int))
print('----------------------------------')
print(contigency_table )
chi2, _, _, _ = chi2_contingency(contigency_table)
n = contigency_table.values.sum()
cramers_v = np.sqrt(chi2/n)
results.append([col, pearson_corr, cramers_v])
print('----------------------------------')
print(tabulate(results, headers = ['criteria', 'Pearsons coefficient', 'cramers_v']))
----------------------------------
Pregnant(Y/N) 0 1
PCOS (Y/N)
0 221 142
1 113 64
----------------------------------
Weight gain(Y/N) 0 1
PCOS (Y/N)
0 280 83
1 56 121
----------------------------------
hair growth(Y/N) 0 1
PCOS (Y/N)
0 316 47
1 76 101
----------------------------------
Skin darkening (Y/N) 0 1
PCOS (Y/N)
0 307 56
1 67 110
----------------------------------
Hair loss(Y/N) 0 1
PCOS (Y/N)
0 220 143
1 75 102
----------------------------------
Pimples(Y/N) 0 1
PCOS (Y/N)
0 222 141
1 54 123
----------------------------------
Fast food (Y/N) 0 1
PCOS (Y/N)
0 223 140
1 38 139
----------------------------------
Reg.Exercise(Y/N) 0 1
PCOS (Y/N)
0 281 82
1 126 51
----------------------------------
criteria Pearsons coefficient cramers_v
-------------------- ---------------------- -----------
Pregnant(Y/N) -0.0286064 0.0245456
Weight gain(Y/N) 0.440488 0.436419
hair growth(Y/N) 0.464245 0.459823
Skin darkening (Y/N) 0.475283 0.471008
Hair loss(Y/N) 0.171913 0.167951
Pimples(Y/N) 0.287802 0.283856
Fast food (Y/N) 0.375389 0.371442
Reg.Exercise(Y/N) 0.0678092 0.0632309
It seems that hair growth, skin darknin and hair loss are correlated with PCOS diagnosis. Fast food seems to have a correlation but I wonder if that is an artefact.
Training a classifier (Random Forest)
I will use a random forrest classifier here because there is no specific knowledge to choose other classifiers. In addition, the data consists of both integers and boolaen types. I believe that random forest classifier should work.
$precision = \frac{TP}{TP+FP}$
$recall = \frac{TP}{FP+FN}$
$F_1 score = \frac{precision \times recall}{precision + recall}$
from sklearn.model_selection import train_test_split, cross_val_predict
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, classification_report, confusion_matrix, precision_recall_curve
from sklearn.preprocessing import StandardScaler
columns_to_convert = df_PCOS_all.filter(like = 'Y/N').columns
df_PCOS_all[columns_to_convert] = df_PCOS_all[columns_to_convert].astype('int')
label_col = "PCOS (Y/N)"
X = df_PCOS_all.drop(columns = [label_col])
X = X.drop(columns = columns_to_drop, axis = 1)
y = df_PCOS_all[label_col]
float_columns = X.select_dtypes(include = ['float64']).columns
scaler=StandardScaler()
X[float_columns] = scaler.fit_transform(X[float_columns])
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
clf = RandomForestClassifier()
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f'Accuracy is {accuracy}')
print('\n Classification report is')
print(classification_report(y_test, y_pred))
# Optional: Display the confusion matrix
conf_matrix = confusion_matrix(y_test, y_pred)
print("\n Confusion Matrix:")
print('\n'.join(['\t'.join([str(cell) for cell in row]) for row in conf_matrix]))
Accuracy is 0.8888888888888888
Classification report is
precision recall f1-score support
0 0.87 0.97 0.92 71
1 0.93 0.73 0.82 37
accuracy 0.89 108
macro avg 0.90 0.85 0.87 108
weighted avg 0.89 0.89 0.89 108
Confusion Matrix:
69 2
10 27
The above scores don’t look too bad.
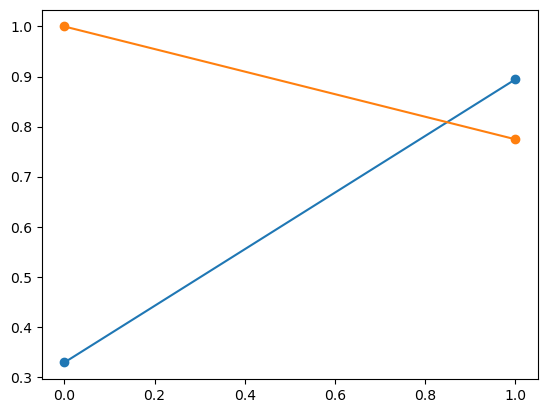
Let us try to make a precisio vs recall curve. The following curve doesn’t look right, so I have to do something to fix it.
y_scores = cross_val_predict(clf, X_train, y_train)#, method = 'decision_function')
precisions, recalls, thresholds = precision_recall_curve(y_train, y_scores)
print(precisions,recalls, thresholds)
plt.plot(thresholds, precisions[:-1])
plt.plot(thresholds, recalls[:-1])
plt.scatter(thresholds, precisions[:-1])
plt.scatter(thresholds, recalls[:-1])
[0.3287037 0.89430894 1. ] [1. 0.77464789 0. ] [0 1]
<matplotlib.collections.PathCollection at 0x15f8de990>
Hypothesis testing (next step)
see https://towardsdatascience.com/hypothesis-testing-with-python-step-by-step-hands-on-tutorial-with-practical-examples-e805975ea96e for hypothesis testing
